Карданный вал, карданные сцепления, карданный подвес — эти вещи сегодня хорошо известны, особенно автомеханикам и специалистам по инерционной навигации. Математики еще знают формулу Кардано, специалисты шифровального дела — «решетки Кардано». Все это — дело рук, или, скорее, ума великого математика, механика, инженера, геолога, астронома — одним словом, энциклопедиста эпохи Возрождения Джероламо Кардано. Впрочем, сам себя он считал прежде всего выдающимся врачом — в автобиографической книге «О моей жизни» даже сравнивал себя с Гиппократом, Галеном и Авиценной!
Происхождение
Он родился 24 сентября 1501 года — ровно 510 лет назад — в древнем городе Павия, на севере Италии. 510 лет — дата, конечно, не «круглая», но и 10 лет назад о полутысячелетнем юбилее одного из наиболее заметных представителей эпохи Ренессанса, кажется, почти никто не вспомнил. Наверное, сказалась временное расстояние: мы охотно отмечает столетние, даже двухсотлетние даты, но дальше вглубь истории почти не заглядываем. Возможно потому, что люди, которые жили так давно, кажутся нам существами полумифическими, даже несмотря на их свершения и достижения. Но они же жили, и о жизни некоторых из них, как например, Кардано, мы знаем достаточно много.
Итак, отец Джероламо Кардано был известным адвокатом, имя которого встречается даже в заметках Леонардо да Винчи, но мальчик родился вне брака. Это очень помешало ему в дальнейшем, поскольку когда после окончания Падуанского университета в 1526 году он пытался получить врачебную практику в Милане, в городскую коллегию врачей его как незаконнорожденного не приняли. Впрочем, лечить он все же начал, но в провинциальном городке Галларт. При этом самоотверженно продолжал исследовать тайны медицины и даже начал писать трактаты на медицинские темы. Однако не только на медицинские, так интересовала его и философия, и астрология, и много чего еще. Примерно в те же времена начал он и карьеру лектора по математике: эта наука привлекала его с детства, и уже в юности он достиг в ней успехов не меньших, а может и больших, чем в медицине. А еще он постоянно совершенствовал мастерство в азартных играх, к которым присоединился еще в юношеские годы. Причем не только играл, но и пытался найти в игре определенные закономерности, что в конце концов вылилось в один из его вполне научных трудов — «Книгу об игре в кости», которая содержала начало теории вероятностей, некоторые вопросы комбинаторики и даже психологии (конечно, игры и игроков). Заметим, что книга была написана, когда он был еще очень молодым человеком — в 1526 году, но выдал он ее только 1563 году.
Его мать неудачно пыталась сделать аборт

Кардано вырос в Павии, в Италии. Его родителями были молодая вдова Клара Мичери и пожилой адвокат Фацио Кардано. Они не были женаты, чтобы избежать скандала в Милане мать отправилась рожать его в Павию. Но перед родами Клара пыталась прервать беременность. Она применяла абортивные средства, которые отразились на здоровье ребенка.
Эрудит эпохи Возрождения
Вообще, книг за свою жизнь он написал очень много. Ведь занимался не только медициной и математикой, но и философией, химией, геологией, минералогией, составлением календарей, астрономией и астрологией и, конечно, изобретательством и конструированием различных технических устройств. Известно 138 его печатных работ общим объемом примерно 7000 страниц большого формата — in folio. Был даже автором своеобразных энциклопедий — книги «О тонких материях» и «О разнообразии вещей». К тому же, около 100 (!) собственных творений он уничтожил сам в ожидании ареста за несколько лет до смерти.
Во всех отраслях, которыми занимался Джероламо Кардано, он достигал немалого успеха. Известно, например, что к услугам его как астролога прибегал даже Папа Римский (в те годы составления гороскопов считалось вполне богоугодным делом). Существует даже версия, что и смерть его была неслучайной: якобы он покончил с собой, чтобы подтвердить собственноручно составленный свой гороскоп. Сведения об особенностях его характера, которые дошли до нашего времени, если не заставляют поверить в эту мрачную легенду, то по крайней мере многое в его жизни объясняют.
Азартный, мстительный, отчаянный, острый на язык, ради достижения цели готов на любые поступки и одновременно благородный и верный в дружбе, Кардано, безусловно, был личностью неординарной. Недаром позже великий немецкий математик и философ Готфрид Вильгельм Лейбниц заметил: «Кардано был великим человеком со всеми его недостатками; без них он был бы совершенным». Справедливости ради стоит отметить, что эти недостатки были следствием тяжелого детства: мать считала его бременем, стеснялась как позора и часто вымещали на нем свой гнев избиением; отец жил отдельно и при встречах также ограничивал воспитательное воздействие шлепками; к тому же и крепким здоровьем Кардано не мог похвастаться ни в детстве, ни в зрелом возрасте. Поэтому то, что другие получали без всяких усилий, ему приходилось в жизни вырывать. Совершенно очевидно, что во многом именно ранний опыт выживания и сформировал в конце концов как положительные, так и отрицательные черты его характера и желание признания.
Последнее было в его жизни чрезвычайно важным. Известно, например, что даже знаменитое устройство, получившее его имя и известное ныне как карданный вал или карданный подвес, появился в 1541 году в результате того, что Кардано (тогда уже ректору городской коллегии врачей) была оказана честь в числе самых почитаемых граждан Милана встречать испанского короля Карла V. Он даже шел у королевского балдахина. Растроганный таким проявлением уважения, он предложил оборудовать экипаж венценосца подвесом из двух валов, взаимное вращение которых не будет выводить карету из горизонтального положения. Правда, идея такого подвеса была известна достаточно давно и даже нашла место в «Атлантическом кодексе» Леонардо да Винчи, однако с этим сводом самых различных сведений почти из всех тогда известных областей знаний образованные люди смогли познакомиться только через два века. А конструкция эта начала применяться все шире в различных вариантах и использоваться в технике именно после обнародования Кардано.
Он всю жизнь был болезненным человеком



Джероламо боролся с плохим здоровьем большую часть своей жизни. В детстве у него были опухоли на лице, в 8 лет он заболел дизентерией. Однажды он упал с лестницы, держа в руках молоток, который разбил ему лоб. Несмотря на слабое здоровье, юноша работал помощником у отца и путешествовал вместе с ним.
Тайна кубических уравнений
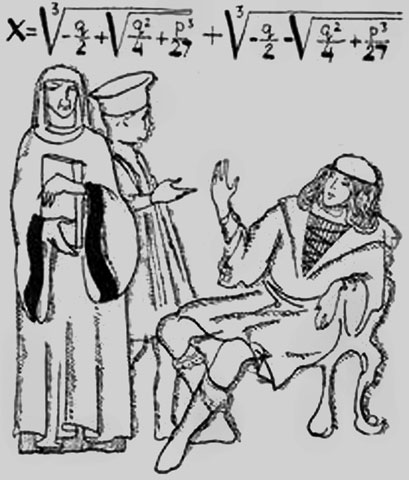


Приблизительно в те же годы Кардано активно занимается математикой. Еще в тридцатые годы он начал работать над большим трактатом по арифметике, первое издание которого вышло в свет 1539 г. «Практика общей арифметики» принесла ему признание в среде знатоков математики, но сам автор ней был не слишком доволен. Причиной было то, что в ней не нашла отражение разгадка одной тогдашней математической тайны, которой он хотя и владел, но не мог обнародовать через обстоятельство, связанное с автором этого открытия.
Речь идет о способе решения кубических уравнений. Или, скорее, о рецептах их решений, потому что к внедрению алгебраической символики оставалось еще более ста лет, и то, как находить корни уравнений, математики объясняли описаниями необходимых действий, часто — стихотворной латынью.
К решению этой проблемы европейские и арабские математикы подбирались несколько веков. В 1494 году известный итальянский ученый Лука Пачоли в книге «Сумма арифметики» — одном из первых печатных математических трактатов, написанных, к тому же, не на латыни, а на итальянском языке, даже авторитетно заявил, что для решения кубических уравнений «искусством алгебры еще не дан способ, как не дано способа квадратуры круга «, и поэтому их следует отнести к числу» невозможных «. Это заявление отвлекло многих математиков от дальнейших попыток все же найти такой способ.
Многих, но не всех.
Примерно в 1515 году профессор Болонского университета Сципио дель Ферро (1456-1526) уже изобрел путь решения кубических уравнений вида х3 + ax = b. Перед смертью свой секрет Ферро открыл только зятю Аннибалу делла Наве и еще своему ученику Антонио Марио Фиоре. Последний решил использовать полученные знания в турнирах по решению различных математических задач, которые тогда были распространены в Европе. Победы в подобных турнирах приносили уважение, денежные награды и возможность получить приличную должность в каком-то из университетов.
Тарталья и его победа



У те же времена к проблеме решения кубических уравнений приступил молодой математик из Вероны Никколо Фонтане, известный в истории науки под прозвищем Тарталья, что в переводе с итальянского значило «заика». Прозвищу этому он был обязан увечью от сабельной раны лица и неба, полученной еще в детстве от французского солдата — одного из завоевателей его родного города Брешии во время войны с венецианцами. Свободно разговаривать после этого он не мог. Но увечье не помешало ему учиться и заниматься наукой. Это был настоящий подвиг, потому что семья его была очень бедной: отец, работавший почтальоном, умер, когда ему было всего шесть лет, у матери кроме него было еще двое детей. Даже школу он посещал лишь 15 дней, а дальше пришлось работать и учиться в то время, когда другие дети играли на улице. И все же, его успехи в математике были настолько значительными, что вскоре он стал зарабатывать на жизнь уроками и консультированием инженеров, артиллеристов, купцов, архитекторов и строителей. Более того, он переводил живым итальянским языком труды Архимеда и Евклида и писал собственные книги, посвященные вопросам практического применения математики и механики.
Как-то за помощью в решении задач, которые сводились к кубическим уравнениям, к нему обратился учитель Брешии где Кои. Тарталья с возмущением отказался — мол, не хочет даже браться за заведомо неразрешимые задачи. Однако задачи его заинтересовали, и через некоторое время Тартальи удалось найти способ построения графика кубического уравнения вида х3 + ax = b и он стал заявлять, что овладел большим алгебраическим секретом. Слухи об этом дошли и до Антонио Фиоре, который воспринял их за простое восхваление невежды. То же самое, кстати, думал о Фиоре и Тарталья, который откуда-то узнал о завещании дель Ферро.
Однако уверенный в своем «тайном оружии», дель Ферро вызвал в 1535 году Тарталью на соревнования, по условиям которых соперники обменивались через нотариуса тридцатью задачами, на решение которых давалось пятьдесят дней. Победителем становился тот, кто решит большее количество задач. Конечно, все 30 задач, которые предложил Фиоре, были кубическими уравнениями с различными коэффициентами. Чтобы отыскать ключ к их решению, Тартальи пришлось приложить максимум усилий. В конце концов, за восемь дней до срока, когда решение нужно было отдать нотариусу, найти способ удалось. Поэтому предложенные задачи он решил в течение двух часов. На следующий день он нашел и способ решения кубических уравнений вида х3 = ах + b, которые в связи с тем, что отрицательными числами в те времена еще не пользовались, считались отличными от приведенного выше. Что касается Фиоре, то с большинством задач, отобранных Тартальей по различным разделам алгебры и геометрии, он так и не справился.
Слух о блестящей победе Тартальи не только над Фиоре, но над математической загадкой веков, быстро распространился по Италии. Кардано, который лелеял амбициозные мечты, что математический трактат, который он тогда только писал, придет на смену классической книге Луки Пачоли, потерял покой. Он начал буквально преследовать Тарталью с просьбой открыть ему свои секреты. Тот упорно отказывался, подозревая даже, что Кардано — подставное лицо, что снял упомянутый выше учитель математики где Кои. Однако, как ни странно, через некоторое время Кардано все же достиг своей цели! Каким образом он заставил Тарталью — человека, по воспоминаниям современников далеко не ангельского характера — расстаться со своей тайной, не совсем понятно. Но факт остается фактом: латинским стихом тот сообщил Кардано о своем рецепте, хотя и без указания никаких намеков на его выведение. Взамен Кардано был вынужден поклясться, что больше никому его не откроет. Поэтому напечатать решение в своей книге он просто не имел права!
Решетка Кардано
Дешифрование методом двойной перестановки Читать далее: Дешифрование методом решетки Кардано
3 Решетка Кардано
Решётка Кардано — инструмент кодирования и декодирования, представляющий собой специальную прямоугольную (в частном случае — квадратную) таблицу-карточку, часть ячеек которой вырезана.
В 1550 году, Джироламо Кардано (1501—1576), предложил простую решетку для шифрования сообщений. Он планировал маскировать сообщения под обычное послание, так что в целом они не были полностью похожи на шифрованные. Такое замаскированное сообщение считается примером стеганографии, которая является подразделом криптографии. Но имя Кардано относилось к решеткам, которые могли и не быть зобретением Кардано, тем не менее, шифры, реализованные с использованием картонных решеток, принято называть решётками Кардано.
Известно, что Кардинал Ришелье (1585—1642) был приверженцем решетки Кардано и использовал её в личной и деловой переписке. Образованные жители Европы XVII века были знакомы с игрой слов в литературе, в том числе с акростихом, анаграммой и шифрами. К концу XVII века первые решетки Кардано уже почти не использовались, но иногда они всё же появлялись в виде зашифрованных посланий и в качестве литературных диковинок. Например, Джордж Гордон Байрон пользовался решеткой Кардано, но скорее для демонстрации литературных навыков, чем для серьёзного шифрования. Решетка содержит отверстия для отдельных символов, а сообщение заполняется набором букв или цифр и представляет собой, очевидно, криптограмму, в то время как Кардано намеревался сделать стеганограмму. Эти решетки с прорезями для букв можно назвать в честь Кардано, но их также называют просто картонными шифровальными решетками.
Одна из разновидностей решётки Кардано — вращающаяся решетка или сетка, в основе которой лежит шахматная доска, которая использовалась в конце XVI века. Вращающаяся решетка снова появилась в более сложной форме в конце XIX века, но, к этому времени, какая-либо связь с Кардано осталась только в названии.
3.1 Шифрование методом решетки Кардано
Описание решетки Кардано.
Решетка Кардано сделана из листа картона или пергамента, или же из тонкого металла. Чтобы обозначить линии письма, бумагу разлиновывают, и между этими линиями вырезают прямоугольные области через интервалы произвольной длины.
Шифратор помещает решетку на лист бумаги и пишет сообщение в прямоугольных отверстиях, в которых помещается отдельный символ, слог или целое слово. При передвижении решётки фрагменты заполняются, образуя запись, искажающую исходное сообщение. Кардано предлагал составлять текст 3 раза для полировки каких-либо шероховатостей, которые могли указывать на скрытые слова.
У получателя сообщения должна быть такая же решетка. Копии решетки вырезаются из первичного шаблона, однако для взаимно-однозначного соответствия можно было бы сделать множество других шаблонов. Решетку можно разместить в 4 положениях — лицом вверх, лицом вниз, вертикально и в перевернутом положении, что вчетверо увеличивает число возможных размещений сетки.
Разместить не относящееся к делу сообщение вокруг скрытого текста на практике может быть трудно. Неестественный язык привлекает к себе внимание, и цель решетки Кардано, согласно Фрэнсису Бэкону, — составить сообщение «без подозрений». Но перед Кардано стояла менее трудная задача, поскольку орфография 16 века не была ограничена столь жесткими стандартами и оставляла больше пространства для каллиграфических сокращений и украшений.
Когда зашифрованное сообщение составлено плохо, оно выделяется неестественным языком и постоянно меняющимся стилем. Специалист может попытаться восстановить решетку, если у него имеется несколько экземпляров подозрительных сообщений из переписки. Когда сообщение зашифровано хорошо, его трудно выявить. Даже если специалист считает сообщение подозрительным, зашифрованный текст может содержать любая невинная буква. Поэтому, на практике, единственное решение — это получить саму решетку.
Чтобы прочитать закодированное сообщение, необходимо наложить решётку Кардано на текст нужное число раз и прочитать буквы, расположенные в вырезанных ячейках. Решётки Кардано предстовляют собой квадратные таблицы, где четверть ячеек прорезана так, что при четырёх поворотах они показывают весь квадрат. Вписание в прорезанные ячейки текста и повороты решётки продолжаются до тех пор, пока весь квадрат не будет заполнен. Например, на рисунке ниже показан процесс шифровки решеткой 4 на 4 :
| С |
| К |
| О |
| Р |
| О |
| _ |
| Б |
| У |
Таблица № 10 0° Таблица № 11 90°
| Д |
| Е |
| Т |
| _ |
| З |
| И |
| М |
| А |
Таблица № 12 180 ° Таблица № 13 270 °
При зашифровке таким способом, мы получили шифр текст: СЗДО_ЕИКТБОМАРУ_.
| С | З | Д | О |
| _ | Е | И | К |
| Т | Б | О | М |
| А | Р | У | _ |
Таблица № 14
Дешифрование методом двойной перестановки Читать далее: Дешифрование методом решетки Кардано
Информация о работе «Основы криптологии»
Раздел: Информатика, программирование Количество знаков с пробелами: 23962 Количество таблиц: 21 Количество изображений: 2
Похожие работы
Исторические основы криптологии
153175
2
11
… зловещую команду: YOU KILL ATONES Кардано использовал квадратную решетку, которая своими вырезами однократно покрывает всю площадь квадрата при ее самосовмещениях. На основе такой решетки он построил шифр перестановки. Нельзя не упомянуть в историческом обзоре имени Матео Ардженти, работавшего в области криптографии в начале XVII в. Он составил руководство по криптографии на 135 листах, …
Криптология: подстановочно-перестановочный шифр и его применение
44234
3
4
… историки считают Иоганна Трисемуса, аббата из Германии, вторым отцом современной криптологии. В 1508 году Трисемус написал «Полиграфию», первую печатную работу по криптологии. В ней он первым систематически описал применение шифрующих таблиц, заполненных алфавитом в случайном порядке. Для получения такого шифра обычно использовались ключевое слово или фраза и таблица, которая для русского языка …
Криптология: точки соприкосновения математики и языкознания
34632
40
0
… . Криптоанализ – наука (и практика ее применения) о методах и способах вскрытия шифров. Криптография и криптоанализ составляют единую область знаний – криптологию, которая в настоящее время является областью современной математики, имеющий важные приложения в современных информационных технологиях. Термин «криптография» ввел Д.Валлис. Потребность шифровать сообщения возникла очень давно. В V – …
Криптография. Шифры, их виды и свойства
28379
1
0
… по их защите, некоторые из них были решены в рамках криптографии, что потребовало развития новых подходов и методов. 2. Шифры, их виды и свойства В криптографии криптографические системы (или шифры) классифицируются следующим образом: симметричные криптосистемы асимметричные криптосистемы 2.1 Симметричные криптографические системы Под симметричными криптографическими системами …